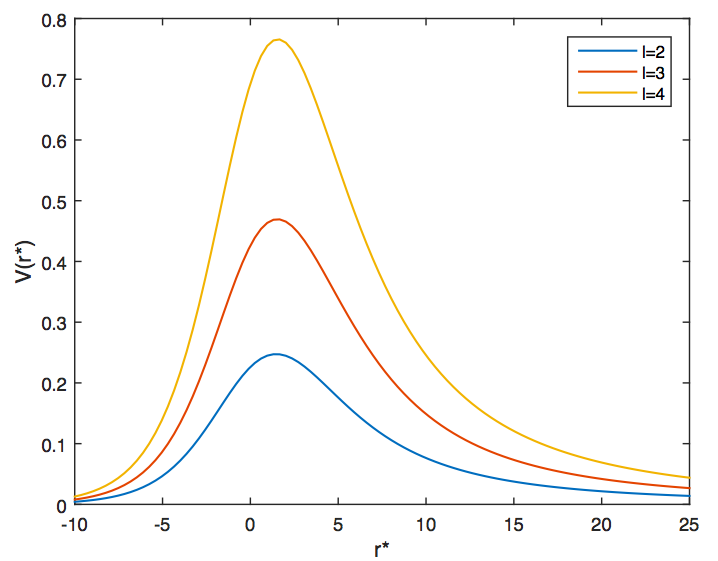
It has already been shown that the gravitational waves emitted from a Schwarzschild black hole in f(R) gravity have no signatures of the modification of gravity from General Relativity, as the Regge–Wheeler equation remains invariant. In this paper we consider the perturbations of Ricci scalar in a vacuum Schwarzschild spacetime, which is unique to higher order theories of gravity and is absent in General Relativity. We show that the equation that governs these perturbations can be reduced to a Volterra integral equation. We explicitly calculate the reflection coefficients for the Ricci scalar perturbations, when they are scattered by the black hole potential barrier. Our analysis shows that a larger fraction of these Ricci scalar waves are reflected compared to the gravitational waves. This may provide a novel observational signature for fourth order gravity.

We consider the scattering of gravitational waves off a Schwarzschild black hole in f(R)f(R) gravity. We show that the reflection and transmission coefficients for tensor waves are the same as in General Relativity. While the scalar waves, which are not present in General Relativity, demonstrate interesting features. The equation that governs these scalar waves can be reduced to a Volterra integral equation. Analysis of this equation shows that a larger fraction of these waves are reflected compared to what one obtains for tensors. This may provide a novel observational signature for fourth order gravity.